1.
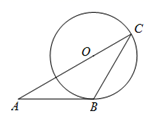
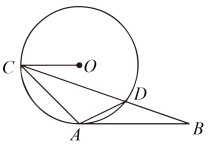
如图,已知⊙O的半径为m,点C在直径AB延长线上,BC=m.在过点C的任一直线l上总存在点P,使过P的⊙O的两切线互相垂直,则∠ACP的最大值等于.

【考点】
勾股定理;
正方形的判定与性质;
切线的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练