1.
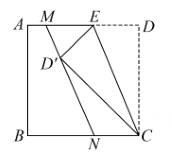
如图,在正方形ABCD中,AB=6,M是AD边上的一点,AM:MD=1:2.将△BMA沿BM对折至△BMN,连接DN,则DN的长是( )

A.
 B.
B.
 C.
3
D.
C.
3
D.

【考点】
直角三角形全等的判定-HL;
正方形的性质;
翻折变换(折叠问题);
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优