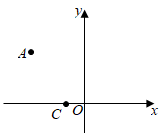
在平面直角坐标系中，点A，D的坐标分别是 .在y轴上取一点C，将线段绕点C逆时针旋转得到 .

0 返回出卷网首页

1. 在平面直角坐标系中，点A，D的坐标分别是 $\text{[math]}$ .在y轴上取一点C，将线段 $\text{[math]}$ 绕点C逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ .

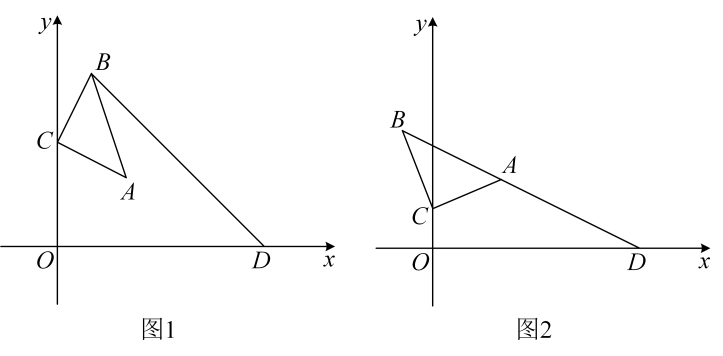
(1) 如图1，若点C的坐标为 $\text{[math]}$ ，求 $\text{[math]}$ 的长.

(2) 如图2，若点A在线段 $\text{[math]}$ 上，求点C的坐标.

(3) 当 $\text{[math]}$ 取得的最小值时，求点C的坐标.

【考点】

坐标与图形性质; 旋转的性质; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 在平面直角坐标系中，点 $\text{[math]}$ 是原点，四边形 $\text{[math]}$ 是矩形，点 $\text{[math]}$ ，点 $\text{[math]}$ .以点 $\text{[math]}$ 为中心，顺时针旋转矩形 $\text{[math]}$ ，得到矩形 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点分别为 $\text{[math]}$ .

(1) 如图①，当点 $\text{[math]}$ 落在 $\text{[math]}$ 边上时，求点 $\text{[math]}$ 的坐标；

(2) 如图②，当点 $\text{[math]}$ 落在线段 $\text{[math]}$ 上时， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ .求点 $\text{[math]}$ 的坐标；

(3) 记 $\text{[math]}$ 为矩形 $\text{[math]}$ 对角线的交点， $\text{[math]}$ 为 $\text{[math]}$ 的面积，求 $\text{[math]}$ 的取值范围（直接写出结果即可）.

综合题困难

2. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．根据所给定义解决下列问题：

(1) 若已知点D（1，2）、E（﹣2，1）、F（0，6），则这3点的“矩面积”=．

(2) 若D（1，2）、E（﹣2，1）、F（0，t）三点的“矩面积”为18，求点F的坐标．

综合题普通

3. 已知如图，四边形ABDC坐标为A（9，0），B（5，1），C（5，4），D（2，4）．

(1) 请在边长为1的小正方形组成的网格中建立平面直角坐标系，然后在平面直角坐标系中画出四边形ABDC．

(2) 求四边形ABDC的面积．

综合题普通