1.
在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“雁点”.例如  ……都是“雁点”.
……都是“雁点”.
(1)
求函数  图象上的“雁点”坐标;
(2)
若抛物线
图象上的“雁点”坐标;
(2)
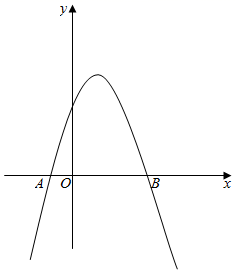
若抛物线  上有且只有一个“雁点”E,该抛物线与x轴交于M、N两点(点M在点N的左侧).当
上有且只有一个“雁点”E,该抛物线与x轴交于M、N两点(点M在点N的左侧).当  时.
(3)
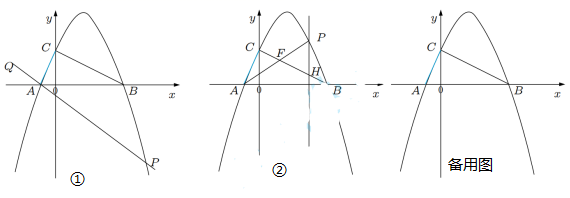
如图,抛物线
时.
(3)
如图,抛物线  与x轴交于A、B两点(点A在点B的左侧),P是抛物线
与x轴交于A、B两点(点A在点B的左侧),P是抛物线  上一点,连接
上一点,连接  ,以点P为直角顶点,构造等腰
,以点P为直角顶点,构造等腰  ,是否存在点P,使点C恰好为“雁点”?若存在,求出点P的坐标;若不存在,请说明理由.
,是否存在点P,使点C恰好为“雁点”?若存在,求出点P的坐标;若不存在,请说明理由.
①求c的取值范围;
②求 的度数;
【考点】
一元二次方程根的判别式及应用;
反比例函数与一次函数的交点问题;
等腰直角三角形;
二次函数与一次函数的综合应用;
二次函数图象上点的坐标特征;
能力提升