已知正方形ABCD与正方形AEFG，正方形AEFG绕点A旋转一周.

0 返回出卷网首页

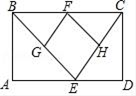
1. 已知正方形ABCD与正方形AEFG，正方形AEFG绕点A旋转一周.

(1) 如图①，连接BG、CF，求 $\text{[math]}$ 的值；

(2) 当正方形AEFG旋转至图②位置时，连接CF、BE，分别去CF、BE的中点M、N，连接MN、试探究：MN与BE的关系，并说明理由；

(3) 连接BE、BF，分别取BE、BF的中点N、Q，连接QN，AE=6，请直接写出线段QN扫过的面积.

【考点】

三角形全等的判定; 正方形的性质; 相似三角形的判定与性质; 等腰直角三角形; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

(1) 证明推断：如图①，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G，求证： $\text{[math]}$ .

(2) 类比探究：如图②，在正方形ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F，若AB＝6，求OF的长；

(3) 拓展运用：若正方形ABCD变为▱ABCD，如图③，连结DE交AC于点G，若四边形OFEG的面积为 $\text{[math]}$ ，求▱ABCD的面积.

综合题困难

2. 已知矩形ABCD中，E是AD边上的一个动点，点F，G，H分别是BC，BE，CE的中点．

(1) 求证：△BGF≌△FHC；

(2) 设AD=a，当四边形EGFH是正方形时，求矩形ABCD的面积．

综合题普通

3. 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D是 $\text{[math]}$ 边上一点（含端点A、B），过点B作 $\text{[math]}$ 垂直于射线 $\text{[math]}$ ，垂足为E，点F在射线 $\text{[math]}$ 上，且 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 如图2，连接 $\text{[math]}$ ，点P、M、N分别为线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、

$\text{[math]}$ 、 $\text{[math]}$ .求 $\text{[math]}$ 的度数及 $\text{[math]}$ 的值；

(3) 在（2）的条件下，若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 面积的最大值.

综合题困难