1.
如图
(1)
证明推断：如图①，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G，求证： 
.
(2)
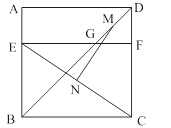
类比探究：如图②，在正方形ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F，若AB＝6，求OF的长；
(3)
拓展运用：若正方形ABCD变为▱ABCD，如图③，连结DE交AC于点G，若四边形OFEG的面积为 
，求▱ABCD的面积.
【考点】
正方形的性质;
相似三角形的判定与性质;
三角形的中位线定理;
能力提升
真题演练
1.
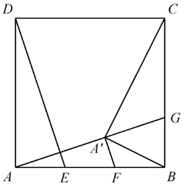
如图，点E是正方形ABCD的边BC延长线上一点，联结DE，过顶点B作BF⊥DE，垂足为F，BF交边DC于点G．
(1)
求证：GD•AB=DF•BG；
(2)
联结CF，求证：∠CFB=45°．
