基础巩固
能力提升
变式训练
拓展培优
真题演练
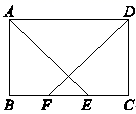

 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).













