1.
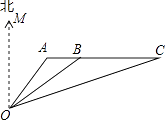
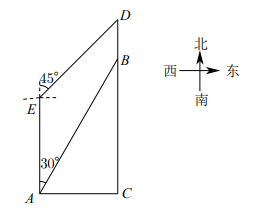
如图,某天我国一艘海监船巡航到  港口正西方的
港口正西方的  处时,发现在
处时,发现在  的北偏东60°方向,相距150海里的
的北偏东60°方向,相距150海里的  处有一可疑船只正沿
处有一可疑船只正沿  方向行驶,点
方向行驶,点  在
在  港口的北偏东30°方向上,海监船向
港口的北偏东30°方向上,海监船向  港口发出指令,执法船立即从
港口发出指令,执法船立即从  港口沿
港口沿  方向驶出,在
方向驶出,在  处成功拦截可疑船只,此时点
处成功拦截可疑船只,此时点  与点
与点  的距离为
的距离为  海里.
海里.

(1)
求点  到直线
到直线  的距离.
(2)
执法船从
的距离.
(2)
执法船从  到
到  航行了多少海里?
航行了多少海里?
【考点】
勾股定理的应用;
解直角三角形的实际应用﹣方向角问题;
能力提升
真题演练