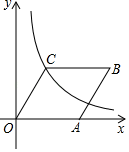
1.
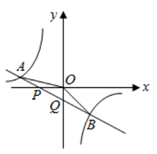
如图,直线  与
与  轴、
轴、  轴相交于
轴相交于  ,
,  两点,与
两点,与  的图象相交于
的图象相交于  ,
,  两点,连接
两点,连接  ,
,  .下列结论:①
.下列结论:①  ;②不等式
;②不等式  的解集是
的解集是  或
或  ;③
;③  ;④
;④  .其中正确的结论是( )
.其中正确的结论是( )
A.
①③
B.
②③④
C.
①③④
D.
②④
【考点】
反比例函数与一次函数的交点问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练