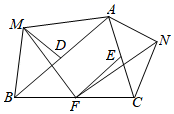
在锐角中，分别以AB和AC为斜边向的外侧作等腰和等腰，点D、E、F分别为边AB、AC、BC的中点，连接MD、MF、FE、FN ．根据题意小明同学画出草图（如图所示），并得出下列结论：① ，② ，③ ，④ ，其中结论正确的个数为（）

0 返回出卷网首页

1. 在锐角 $\text{[math]}$ 中，分别以AB和AC为斜边向 $\text{[math]}$ 的外侧作等腰 $\text{[math]}$ 和等腰 $\text{[math]}$ ，点D、E、F分别为边AB、AC、BC的中点，连接MD、MF、FE、FN ．根据题意小明同学画出草图（如图所示），并得出下列结论：① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$ ，④ $\text{[math]}$ ，其中结论正确的个数为（）

A. 4 B. 3 C. 2 D. 1

【考点】

相似三角形的判定与性质; 三角形的综合; 三角形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题困难

1. 如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 边上， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（　　）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 如图是某晾衣架的侧面示意图，根据图中数据，则C、D两点间的距离是（）

A. 0.9m B. 1.2m C. 1.5m D. 2.5m

单选题容易

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则AC的长为（）

A. 6 B. 8 C. 10 D. 12

单选题容易