1.
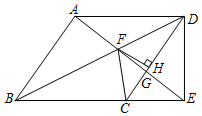
如图,在菱形ABCD中,点F在线段CD上,连接EF,且∠CBE+∠EFC=180°,DF=2,FC=3.则DB=( )

A.
6
B.
 C.
5
D.
C.
5
D.

【考点】
等腰三角形的性质;
菱形的性质;
相似三角形的判定与性质;