1.
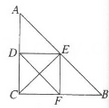
如图所示,在△ABC中,D,E,F分别是AC,AB,BC的中点,且CE=  AB.
AB.
求证:四边形CFED是矩形.
【考点】
平行四边形的判定;
矩形的判定;
三角形的中位线定理;
基础巩固
能力提升
变式训练
拓展培优