如图，抛物线y＝ax2＋5x＋c交x轴于点A（1，0）、B，交y轴于点C（0，﹣4）．

0 返回出卷网首页

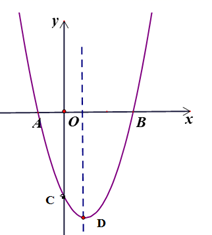
1. 如图，抛物线y＝ax²＋5x＋c交x轴于点A（1，0）、B，交y轴于点C（0，﹣4）．

(1) 求该抛物线的表达式；

(2) 若P是抛物线上x轴上方的一动点，过P作PM⊥x轴，垂足为M．是否存在P点，使得以A，P，M为顶点的三角形与△OBC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

【考点】

待定系数法求二次函数解析式; 相似三角形的性质; 二次函数图象上点的坐标特征;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H.

(1) 求该抛物线的解析式；

(2) 当点P在直线BC上方时，请用含m的代数式表示PG的长度；

(3) 在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由.

综合题困难

2. 如图，抛物线W与x轴交于A(1，0)，M(﹣3，0)两点，交y轴于点B(0，3)，抛物线W关于y轴的对称图形为抛物线L.

(1) 求抛物线W的表达式；

(2) 如果E是点A关于原点的对称点，D是抛物线L的顶点，那么在x轴上是否存在点P，使得△PAD与△EBO是相似三角形？若存在，求出符合条件的点P坐标；若不存在，请说明理由.

综合题普通

3. 已知抛物线L： $\text{[math]}$ 过点 $\text{[math]}$ 和 $\text{[math]}$ ，与x轴的交点为A、B（点A在点B的左侧）.

(1) 求抛物线L的表达式；

(2) 若点P在抛物线L上，点E、F在抛物线L的对称轴上，D是抛物线L的顶点，要使 $\text{[math]}$ （P的对应点是D），且 $\text{[math]}$ .求满足条件的点P的坐标.

综合题普通