1.
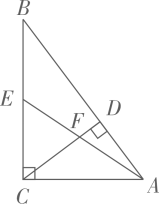
如图,在 中,
中, ,
,  ,
,  , 在
, 在 的内部作
的内部作 交边
交边 于点
于点 ,
,  , 则
, 则 的面积是.
的面积是.

【考点】
三角形的面积;
勾股定理;
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练