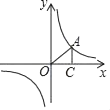
如图，矩形ABCD的边平行于坐标轴，对角线BD经过坐标原点，点C在反比例函数y=的图象上.若点A的坐标为（﹣2，﹣2），则k=（）

0 返回出卷网首页

1. 如图，矩形ABCD的边平行于坐标轴，对角线BD经过坐标原点，点C在反比例函数y= $\text{[math]}$ 的图象上.若点A的坐标为（﹣2，﹣2），则k=（）

A. 2 B. 4 C. 8 D. 16

【考点】

反比例函数系数k的几何意义; 矩形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，设点 $\text{[math]}$ 是函数 $\text{[math]}$ 的图象上成中心对称的两个任意点，斜边为 $\text{[math]}$ ，两条直角边分别平行于 $\text{[math]}$ 轴的直角 $\text{[math]}$ 的面积为（）

A. 2 B. 4 C. 8 D. 随点 $\text{[math]}$ 的变化而变化

单选题容易

2. 如图， $\text{[math]}$ 是双曲线 $\text{[math]}$ 上的一点，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，垂足为 $\text{[math]}$ ，交双曲线于点 $\text{[math]}$ ，则 $\text{[math]}$ 的面积是( )

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，P是反比例函数图象上第二象限内一点，若矩形PEOF的面积为3，则反比例函数的解析式是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易