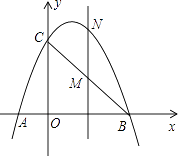如图，抛物线y=ax2+bx-4经过A（-2，0）、B（4，0）两点，与y轴交于点C．点P为线段AB上的一动点（不与点B重合），连接PC、BC，将△BPC沿直线BC翻折得到△BP'C，P'C交抛物线于另一点Q，连接QB．

0 返回出卷网首页

1. 如图，抛物线y=ax²+bx-4经过A（-2，0）、B（4，0）两点，与y轴交于点C．点P为线段AB上的一动点（不与点B重合），连接PC、BC，将△BPC沿直线BC翻折得到△BP'C，P'C交抛物线于另一点Q，连接QB．

(1) 求抛物线的解析式；

(2) 求四边形QCOB面积的最大值：

(3) 当CQ：QP'=1：2时，求点Q的坐标．

【考点】

待定系数法求一次函数解析式; 二次函数的最值; 待定系数法求二次函数解析式; 两条直线被一组平行线所截，所得的对应线段成比例;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知抛物线经过点A（﹣1，0）、B（3，0）、C（0，3）三点．

(1) 求抛物线的解析式．

(2) 点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，请用m的代数式表示MN的长．

(3) 在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．

综合题困难

2. 如图，在平面直角坐标系xOy中，直线 $\text{[math]}$ 与x轴、y轴分别交于点A、B．抛物线 $\text{[math]}$ （a≠0）经过点A，且与y轴相交于点C，∠OCA=∠OAB．

(1) 求直线AB的表达式；

(2) 如果点D在线段AB的延长线上，且AD=AC．求经过点D的抛物线 $\text{[math]}$ 的表达式；

(3) 如果抛物线 $\text{[math]}$ 的对称轴与线段AB、AC分别相交于点E、F，且EF=1，求此抛物线的顶点坐标．

综合题普通

3. 某商品的进价为每件40元，在销售过程中发现，每周的销售量y（件）与销售单价x（元）之间的关系可以近似看作一次函数 $\text{[math]}$ ，且当售价定为50元/件时，每周销售30件，当售价定为70元/件时，每周销售10件．

(1) 求k ， b的值；

(2) 求销售该商品每周的利润w（元）与销售单价x（元）之间的函数解析式，并求出销售该商品每周可获得的最大利润．

综合题普通