1.
如图


【问题情境】
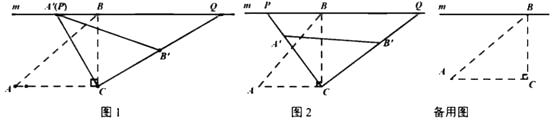
在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中 ,
,
.
【问题探究】
小昕同学将三角板 绕点
按顺时针方向旋转.
(1)
如图2,当点  落在边
落在边  上时,延长
上时,延长  交
交  于点
于点  ,求
,求  的长.
(2)
若点
的长.
(2)
若点  、
、  、
、  在同一条直线上,求点
在同一条直线上,求点  到直线
到直线  的距离.
(3)
连接
的距离.
(3)
连接  ,取
,取  的中点
的中点  ,三角板
,三角板  由初始位置(图1),旋转到点
由初始位置(图1),旋转到点  、
、  、
、  首次在同一条直线上(如图3),求点
首次在同一条直线上(如图3),求点  所经过的路径长.
(4)
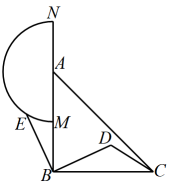
如图4,
所经过的路径长.
(4)
如图4,  为
为  的中点,则在旋转过程中,点
的中点,则在旋转过程中,点  到直线
到直线  的距离的最大值是.
的距离的最大值是.
【考点】
三角形的面积;
勾股定理;
弧长的计算;
解直角三角形;
旋转的性质;
能力提升