1.
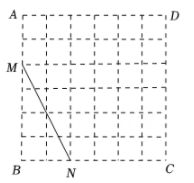
在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值是( )
A.
 B.
6
C.
B.
6
C.
 D.
D.

【考点】
直角三角形全等的判定-HL;
勾股定理;
等腰直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练