1.
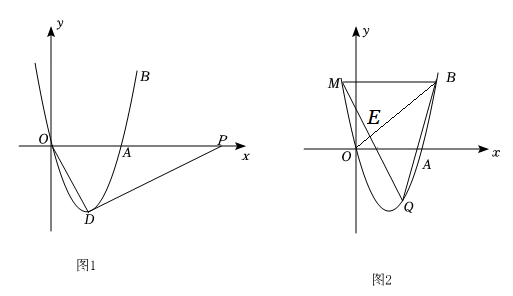
抛物线y=x2-4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.
(1)
直接写出点B和点D的坐标;
(2)
如图1,连接OD,P为x轴上的动点,当tan∠PDO= 时,求点P的坐标;
(3)
如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2 , 求
时,求点P的坐标;
(3)
如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2 , 求 的最大值.
的最大值.
【考点】
锐角三角函数的定义;
二次函数与一次函数的综合应用;
二次函数-动态几何问题;
能力提升
真题演练