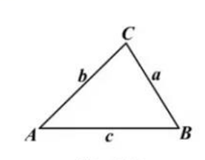
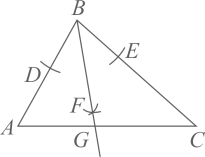
如图为三角形纸片ABC，其中D点和E点将AB三等分，F点为DE中点．若小慕从AB上的一点P，沿着与直线BC平行的方向将纸片剪开后，剪下的小三角形纸片面积为△ABC的，则下列关于P点位置的叙述正确的是（）

1. 古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式，称为海伦-秦九韶公式：如果一个三角形的三边长分别是a，b，c，记 $\text{[math]}$ ，那么三角形的面积为 $\text{[math]}$ .如图，在△ABC中，∠A，∠B，∠C所对的边分别记为a，b，c，若 $\text{[math]}$ ，则△ABC的面积为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. 18 D. $\text{[math]}$

单选题容易

2. 如图，在△ABC中，AB＝2，BC＝4，△ABC的高AD与CE的比为（）

A. 1：2 B. 2：1 C. 1：4 D. 4：1

单选题容易

3. 如图的4×4的方格纸中有一格点△ABC，其面积等于 $\text{[math]}$ cm² ，则这个方格纸的面积等于（）

A. 16cm² B. 20cm² C. 21cm² D. 24cm²

单选题容易

1. 如图，点D，E分别在AB、AC上，BE，CD相交于点F，设S_{四边形EADF}＝S₁ ， S_△BDF＝S₂ ， S_△BCF＝S₃ ， S_△CEF＝S₄ ，则S₁S₃与S₂S₄的大小关系是（）

A. 不能确定 B. S₁S₃＜S₂S₄ C. S₁S₃＝S₂S₄ D. S₁S₃＞S₂S₄

单选题普通

2. 如图，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在一次函数 $\text{[math]}$ 的图象上，它们的横坐标依次为-1，1，2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积和是（）

A. 1 B. 3 C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

3.

如图，在△ABC中，∠ACB=90°，AC=4，BC=2，P是AB边上一动点，PD⊥AC于点D，点E在P的右侧，且PE=1，连结CE．P从点A出发，沿AB方向运动，当E到达点B时，P停止运动．在整个运动过程中，图中阴影部分面积S₁+S₂的大小变化情况是（）

A. 一直减小 B. 一直不变 C. 先增大后减小 D. 先减小后增大

单选题普通

1. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中，给出了著名的秦九韶公式，也叫三斜求积公式，即如果一个三角形的三边长分别为a，b，c，则该三角形的面积为S= $\text{[math]}$ ．现已知△ABC的三边长分别为1，2， $\text{[math]}$ ，则△ABC的面积为．

填空题容易

2. 在△ABC中，AB＝6，AC＝8，△ABC的面积为12 $\text{[math]}$ ，则∠A＝．

填空题普通

3. 如图，四边形ABCD中，E、F、G、H依次是各边中点，O是四边形内一点，若S_四边形_AEOH=3，S_四边形_BFOE=4，S_四边形_CGOF=5，则S_四边形_DHOG=．

填空题困难

1. 如图1，已知等腰三角形ABC的外接圆圆心为点 $\text{[math]}$ 为 $\text{[math]}$ 的直径，AD交BC于点 $\text{[math]}$ ；

(1) 求AB的长；

(2) 连OC ，求证：四边形ABOC为菱形；

(3) 直接写出图2中阴影部分的面积.

解答题困难

2.

(1) 【新知探究】

对于正数 $\text{[math]}$ ，我们称 $\text{[math]}$ 为 $\text{[math]}$ 的算术平均数，称 $\text{[math]}$ 为 $\text{[math]}$ 的几何平均数．请观察下面的表格，并解答下面的问题：

$\text{[math]}$ 的值	$\text{[math]}$ 的值	$\text{[math]}$ 的值
$\text{[math]}$	5	4
$\text{[math]}$	4	4
$\text{[math]}$	4	m
$\text{[math]}$	3	$\text{[math]}$

①表格中的 $\text{[math]}$ ▲ ；

②根据表格，猜想 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系（）；

A $\text{[math]}$ $\text{[math]}$ B $\text{[math]}$ $\text{[math]}$ C $\text{[math]}$ $\text{[math]}$ D $\text{[math]}$ $\text{[math]}$

③当 $\text{[math]}$ 满足条件： ▲ 时， $\text{[math]}$ ；

(2) 【理解应用】

①已知， $\text{[math]}$ ，当 $\text{[math]}$ ▲ 时，代数式 $\text{[math]}$ 取得最大值是 ▲ ；

②如图1，已知，在Rt $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 周长的最大值．

(3) 【拓展提升】

如图2，已知正方形ABCD的边长为4， $\text{[math]}$ 为CD边上的动点，PA交BD于 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交BC边于点 $\text{[math]}$ ，连AF交BD于点 $\text{[math]}$ ，则 $\text{[math]}$ 面积的最小值是 ▲ ．