1.
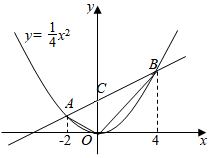
如图,抛物线 与x轴交于A、B两点,与y轴交于点C,已知点
与x轴交于A、B两点,与y轴交于点C,已知点 , 抛物线的对称轴是直线
, 抛物线的对称轴是直线 , 连接
, 连接 、
、 .
.

(1)
用含a的代数式求 ;
(2)
若
;
(2)
若 , 求抛物线的函数表达式:
(3)
在(2)的条件下,当
, 求抛物线的函数表达式:
(3)
在(2)的条件下,当 时,y的最小值是-2,求m的值.
时,y的最小值是-2,求m的值.
【考点】
三角形的面积;
二次函数y=ax²+bx+c的性质;
能力提升
真题演练