1.
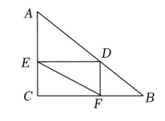
如图,在△ABC中,∠C=90°,AC=6,BC=8,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于__.
【考点】
垂线段最短及其应用;
矩形的性质;