1.
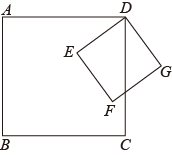
如图,E是正方形ABCD对角线BD上一点.连接AE,CE,并延长CE交AD于点F.若∠AEC=140°,求∠DFE的度数.

【考点】
正方形的性质;
三角形全等的判定-SAS;