1.
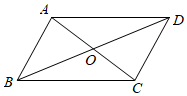
在平行四边形ABCD中,对角线AC,BD交于点O,只需添加一个条件,即可证明平行四边形ABCD是矩形,这个条件可以是(写出一个即可).
【考点】
矩形的判定;
基础巩固
能力提升
变式训练
拓展培优
真题演练