0 返回出卷网首页
1. 如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB＝60°，DC＝EF.

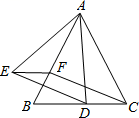
(1) 求证：四边形EFCD是平行四边形；
(2) 若BF＝EF，求证：AE＝AD.
【考点】
等边三角形的性质; 平行四边形的判定; 三角形全等的判定-SAS;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE，已知：∠BAC=30°，EF⊥AB，垂足为F，连接DF．

(1) 试说明AC=EF；
(2) 求证：四边形ADFE是平行四边形．
综合题 普通
2. 如图，在等边△ABC中，D是BC的中点，以AD为边向左侧作等边△ADE，边ED与AB交于点G.

(1) 求∠CAE 的度数；
(2) 取AB的中点F，连接CF，EF，求证：四边形CDEF是平行四边形.
综合题 普通
3. 已知∠ABC＝60°，点F在直线BC上，以AF为边作等边三角形AFE，过点E作ED⊥AB于点D．请解答下列问题：

 

(1) 如图①，求证：AB＋BF＝2BD；
(2) 如图②、图③，线段AB，BF，BD又有怎样的数量关系？请写出你的猜想，不需要证明．
综合题 普通