1.
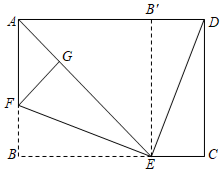
已知正方形 的边长为
的边长为 , 点E是边
, 点E是边 上一点,
上一点, , 连接
, 连接 , 将
, 将 绕点D旋转
绕点D旋转 , 得到
, 得到 , 则
, 则 的面积为.
的面积为.
【考点】
三角形全等及其性质;
三角形全等的判定;
旋转的性质;