1.
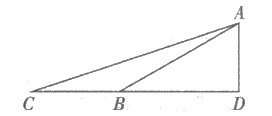
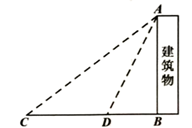
宜宾的夹镜楼建于清代初年,有诗曰:“两水夹明镜,双桥落彩虹;巍峨夹镜楼,一楼镇三江,”左摸蜿蜒岷江,右环湍急金沙,背负千年宜宾之厚重繁华,足启千里南丝绸之路起点;汇岷江金沙江奔涌激流,千古风流,还看“万里长江第一楼”!为此深受某数学小组的喜欢,决定要去测量夹镜楼的高度,已知测角仪高度 为1.6米.他们在A处测得楼顶P处的仰角为
为1.6米.他们在A处测得楼顶P处的仰角为 , 再向楼的方向前进
, 再向楼的方向前进 米到B点,再测得楼顶P处的仰角为
米到B点,再测得楼顶P处的仰角为 , 你能帮助他们算出了夹镜楼的高度吗?(结果保留根号)
, 你能帮助他们算出了夹镜楼的高度吗?(结果保留根号)


【考点】
锐角三角函数的定义;
基础巩固
能力提升
变式训练
拓展培优
真题演练