1.
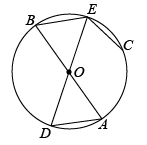
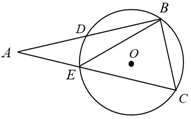
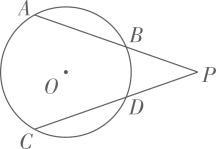
在同圆或等圆中,如果两个圆心角、两条、两条、两条中有一对量相等,那么它们所对应的其余各对量都相等.
【考点】
圆心角、弧、弦的关系;
基础巩固
能力提升
变式训练
拓展培优
真题演练