0 返回出卷网首页
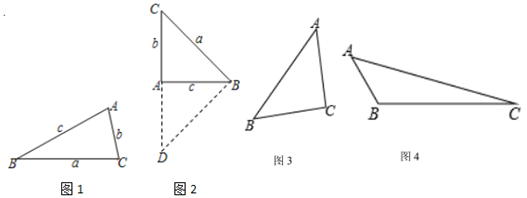
1. 已知：如图，在Rt△ABC中，∠ABC＝90°，AB＝BC ， 将△ABC绕点A逆时针旋转一个角度α得到Rt△ADE ， 连接BD ， CE ．

(1) 如图①，当0°＜α＜45°时，求证：△ABD∽△ACE；
(2) 如图②，当α＝45°时，点E在AB的延长线上，延长DB交CE于点F ， 求∠DFE的度数；
(3) 如图③，当45°＜α＜90°时，延长DB交CE于点F ， 求证：点F是线段CE的中点．
【考点】
三角形内角和定理; 三角形全等及其性质; 三角形全等的判定; 等腰三角形的性质; 相似三角形的判定与性质; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. （发现问题）

(1) 如图1，已知△CAB和△CDE均为等边三角形，D在AC上，E在CB上，易得线段AD和BE的数量关系是．
(2) 将图1中的△CDE绕点C旋转到图2的位置，直线AD和直线BE交于点F ．

①判断线段AD和BE的数量关系，并证明你的结论；

②图2中∠AFB的度数是．
(3) （探究拓展）如图3，若△CAB和△CDE均为等腰直角三角形，∠ABC＝∠DEC＝90°，AB＝BC ， DE＝EC ， 直线AD和直线BE交于点F ， 分别写出∠AFB的度数，线段AD、BE间的数量关系．
综合题 困难
2. 如图，已知在△ABC中，AB＝AC＝6，BC＝5，D是AB上一点，BD＝2，E是BC上一动点，联结DE，并作∠DEF＝∠B，射线EF交线段AC于F.

(1) 求证：△DBE∽△ECF；
(2) 当F是线段AC中点时，求线段BE的长；
(3) 联结DF，如果△DEF与△DBE相似，求FC的长.
综合题 普通
3. 我们定义：三角形中，如果有一个角是另一个角的2倍，那么称这个三角形是2倍角三角形.

(1) 定义应用

如果一个等腰三角形是2倍角三角形，则其底角的度数为；
(2) 性质探索

小思同学通过从“特殊到一般”的过程，对2倍角三角形进行研究，得出结论：

如图1，在△ABC中，如果∠A＝2∠B，那么BC2＝AC（AB＋AC）.

下面是小思同学对其中一种特殊情形的证明方法.

已知：如图2，在△ABC中，∠A＝90°，∠B＝45°.

求证：BC2＝AC（AB＋AC）.

证明：如图2，延长CA到D，使得AD＝AB，连接BD.

∴∠D＝∠ABD，AB＋AC＝AD＋AC＝CD

∵∠CAB＝∠D＋∠ABD＝2∠D，∠CAB＝90°

∴∠D＝45°，

∵∠ABC＝45°，

∴∠D＝∠ABC，又∠C＝∠C

∴△ABC∽△BCD

∴

∴BC2＝AC•CD

∴BC2＝AC（AB＋AC）

根据上述材料提供的信息，请你完成下列情形的证明：

已知：如图1，在△ABC中，∠A＝2∠B.

求证：BC2＝AC（AB＋AC）.

证明：
(3) 性质应用

已知：如图3，在△ABC中，∠C＝2∠B，AB＝12，BC＝10，则AC＝；
(4) 拓展应用

已知：如图4，在△ABC中，∠ABC＝3∠A，AC＝6，BC＝4，求AB的长.
综合题 困难