1.
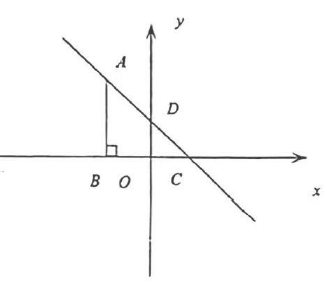
如图,一次函数 的图象与
的图象与 轴和
轴和 轴分别交于点
轴分别交于点 和点
和点 , 且
, 且 .
.
(1)
求 的值;
(2)
若将一次函数
的值;
(2)
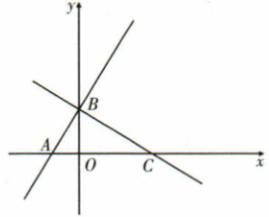
若将一次函数 的图象绕点
的图象绕点 顺时针旋转90°,所得的直线与
顺时针旋转90°,所得的直线与 轴交于点
轴交于点 , 且
, 且 , 求点
, 求点 的坐标;
(3)
在(2)的条件下,若
的坐标;
(3)
在(2)的条件下,若 是
是 轴上任意一点,当
轴上任意一点,当 是以
是以 为腰的等腰三角形时,请求出点
为腰的等腰三角形时,请求出点 的坐标.
的坐标.
【考点】
待定系数法求一次函数解析式;
三角形的面积;
等腰三角形的性质;
勾股定理;
一次函数图象与坐标轴交点问题;
能力提升