1.
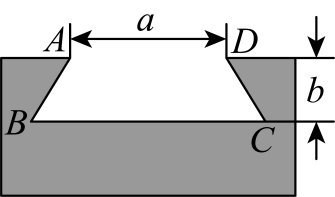
榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面 是梯形,其中
是梯形,其中 ,
,  , 燕尾角
, 燕尾角 , 外口宽
, 外口宽 , 榫槽深度是
, 榫槽深度是 , 则它的里口宽
, 则它的里口宽 为( )
为( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
矩形的判定与性质;
解直角三角形的其他实际应用;









