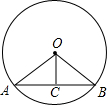
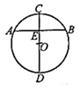
图1是圆形背景墙，两个装饰物放在水平架上，正面示意图如图2所示，为弦，点在圆上，，为的中点，，点，，在同一直线上．测得，，，则圆的直径长为．

0 返回出卷网首页

1. 图1是圆形背景墙，两个装饰物放在水平架上，正面示意图如图2所示， $\text{[math]}$ 为弦，点 $\text{[math]}$ 在圆上， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上．测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则圆的直径长为 $\text{[math]}$ ．

【考点】

勾股定理; 垂径定理; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题困难

1. 《九章算术》是中国传统数学重要的著作之一，其中第九卷《勾股》中记载了一个“圆材埋壁”的问题：“今有圆材，埋在壁中，不知大小．以锯锯之、深一寸，锯道长一尺，问径几何？”用几何语言表达为：如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 寸， $\text{[math]}$ 寸，则半径 $\text{[math]}$ 长为寸．

填空题容易

2. 如图，已知在半径为10的⊙O中，弦AB=16，OC⊥AB ，则OC的长为.

填空题容易

3. 如图， $\text{[math]}$ 的弦AB和直径CD交于点E，且CD平分AB，已知AB=8，CE=2，那么 $\text{[math]}$ 的半径长是．

填空题容易