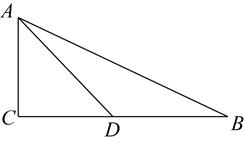
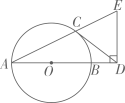
构建几何图形解决代数问题是“数形结合”思想的重要性，在计算时，如图．在中，，延长CB使，连接AD ，得，所以．类比这种方法，计算的值为（）

0 返回出卷网首页

1. 构建几何图形解决代数问题是“数形结合”思想的重要性，在计算 $\text{[math]}$ 时，如图．在 $\text{[math]}$ 中， $\text{[math]}$ $\text{[math]}$ ，延长CB使 $\text{[math]}$ ，连接AD ，得 $\text{[math]}$ $\text{[math]}$ ，所以 $\text{[math]}$ $\text{[math]}$ ．类比这种方法，计算 $\text{[math]}$ 的值为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

等腰三角形的判定; 勾股定理; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D在 $\text{[math]}$ 边上， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 在Rt△ABC中，∠C＝90°，若BC＝3，AC＝4，则sinB的值为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 在Rt△ABC中，∠C＝90°，若AB＝ $\text{[math]}$ ，BC＝2，则sinB的值为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. 2

单选题容易