1.
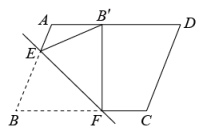
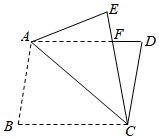
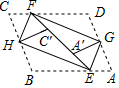
在平行四边形 中,
中, 是锐角,将
是锐角,将 沿直线
沿直线 翻折至
翻折至 所在直线,对应点分别为
所在直线,对应点分别为 ,
,  , 若
, 若 , 则
, 则 .
.
【考点】
平行四边形的性质;
翻折变换(折叠问题);
基础巩固
能力提升
变式训练
拓展培优
真题演练