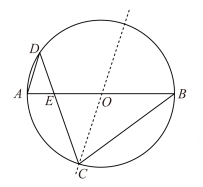
如图，抛物线（其中）与x轴交于A、B两点，交y轴于点C．（1）直接写出的度数和线段AB的长（用a表示）；（2）若点D为的外心，且与的周长之比为，求此抛物线的解析式；（3）在（2）的前提下，试探究抛物线上是否存在一点P，使得？若存在，求出点P的坐标；若不存在，请说明理由．

0 返回出卷网首页

1. 如图，抛物线 $\text{[math]}$ （其中 $\text{[math]}$ ）与x轴交于A、B两点，交y轴于点C．

（1）直接写出 $\text{[math]}$ 的度数和线段AB的长（用a表示）；

（2）若点D为 $\text{[math]}$ 的外心，且 $\text{[math]}$ 与 $\text{[math]}$ 的周长之比为 $\text{[math]}$ ，求此抛物线的解析式；

（3）在（2）的前提下，试探究抛物线 $\text{[math]}$ 上是否存在一点P，使得 $\text{[math]}$ ？若存在，求出点P的坐标；若不存在，请说明理由．

【考点】

圆周角定理; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 如图，A、B、C点在圆O上，若∠ACB=36°，则∠AOB=．

填空题容易

2. 为了估计河的宽度，勘测人员在河的对岸选定一个目标点A ，在近岸分别取点B、D、E、C ，使点A、B、D在一条直线上，且AD⊥DE ，点A、C、E也在一条直线上，且DE∥BC ．经测量BC＝25米，BD＝12米，DE＝40米，求河的宽度AB为多少米？

解答题容易

3. 如图， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .求证： $\text{[math]}$ .

证明题容易