1.
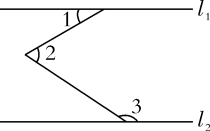
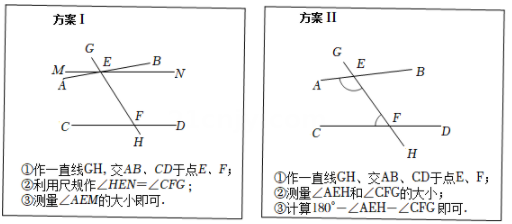
如图所示,下列推理及括号中所注明的推理依据正确的是( )

A.
∵ , ∴
, ∴ (内错角相等,两直线平行)
B.
∵
(内错角相等,两直线平行)
B.
∵ , ∴
, ∴ (两直线平行,内错角相等)
C.
∵
(两直线平行,内错角相等)
C.
∵ , ∴
, ∴ (两直线平行,同旁内角互补)
D.
∵
(两直线平行,同旁内角互补)
D.
∵ , ∴
, ∴ (两直线平行,同位角相等)
(两直线平行,同位角相等)
【考点】
平行线的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练