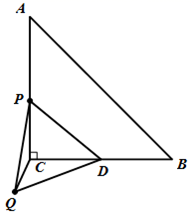
1.
如图,在 中,
中, ,
,  , 点
, 点 是
是 边的中点,点
边的中点,点 是
是 边上一个动点,连接
边上一个动点,连接 , 以
, 以 为边在
为边在 的下方作等边三角形
的下方作等边三角形 , 连接
, 连接 , 则
, 则 的最小值是( )
的最小值是( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
等边三角形的性质;
含30°角的直角三角形;
三角形全等的判定-SAS;