1.
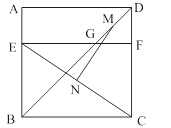
如图,正方形 的对角线相交于点O,点E在
的对角线相交于点O,点E在 边上,连接
边上,连接 , 作
, 作 于点F,连接
于点F,连接 , 若
, 若 ,
,  , 则点O到
, 则点O到 的距离为( )
的距离为( )

A.
 B.
B.
 C.
2
D.
C.
2
D.

【考点】
勾股定理;
正方形的性质;
三角形的中位线定理;