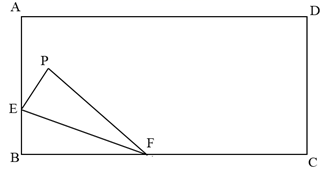
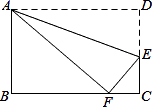
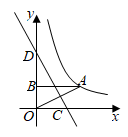
在中，，，点P是线段CB上的一个动点（不与点B，C重合），过点P作直线交AB于点Q．给出如下定义：若在AC边上存在一点M，使得点M关于直线l的对称点N恰好在的边上，则称点M是的关于直线l的“反称点”．例如，图1中的点M是的关于直线l的“反称点”．（1）如图2，若，点，，，在AC边上且，，，．在点，，，中，是的关于直线l的“反称点”为______；（2）若点M是的关于直线l的“反称点”，恰好使得是等腰三角形，求AM的长；（3）存在直线l及点M，使得点M是的关于直线l的“反称点”，直接写出线段CP的取值范围．

1. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地．送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千 $\text{[math]}$ 静止的时候，踏板离地高一尺（ $\text{[math]}$ 尺），将它往前推进两步（ $\text{[math]}$ 尺），此时踏板升高离地五尺（ $\text{[math]}$ 尺），求秋千绳索（ $\text{[math]}$ 或 $\text{[math]}$ ）的长度．

综合题容易

2. 在△ABC中，∠C=30°，AC=4cm，AB=3cm，求BC的长.

解答题容易

3. 如图，某测量小组为了测量山BC的高度，在地面A处测得山顶B的仰角45°，然后沿着坡度为 $\text{[math]}$ 的坡面AD走了200米达到D处，此时在D处测得山顶B的仰角为60°，求山高BC（结果保留根号）．

解答题容易

1. 在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 的半径为 $\text{[math]}$ ，给定直线 $\text{[math]}$ 与点 $\text{[math]}$ ，对于不在直线 $\text{[math]}$ 上的点 $\text{[math]}$ 给出如下定义：作点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ ，若点 $\text{[math]}$ 位于 $\text{[math]}$ 上或 $\text{[math]}$ 内，且点 $\text{[math]}$ 到定点 $\text{[math]}$ 的距离 $\text{[math]}$ 为所有符合条件的 $\text{[math]}$ 中的最大值或最小值，则称点 $\text{[math]}$ 为点 $\text{[math]}$ 关于直线 $\text{[math]}$ 与 $\text{[math]}$ 的“反射极值点”，对应最大值的点称为“反射极大值点”，对应最小值的点称为“反射极小值点”．

(1) 已知直线 $\text{[math]}$ ．

$\text{[math]}$ 点 $\text{[math]}$ ，在点 $\text{[math]}$ 中，点 $\text{[math]}$ 关于直线 $\text{[math]}$ 与 $\text{[math]}$ 的“反射极值点”是______；

$\text{[math]}$ 若点 $\text{[math]}$ 为直线 $\text{[math]}$ 上的动点，且点 $\text{[math]}$ 到其关于直线 $\text{[math]}$ 与 $\text{[math]}$ 的“反射极大值点”与“反射极小值点”的距离之比为 $\text{[math]}$ ，直接写出点 $\text{[math]}$ 的坐标；