1.
 和
和 是两个全等的三角形,
是两个全等的三角形, 绕点A旋转,
绕点A旋转, ,
,  ,
,  .
.

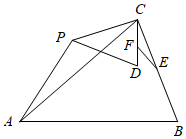
(1)
如图1连接 ,
,  , 在
, 在 绕点A旋转过程中,求
绕点A旋转过程中,求 的值;
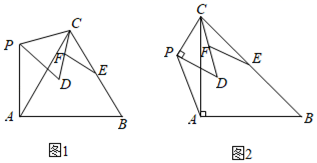
(2)
如图2,在
的值;
(2)
如图2,在 绕点A旋转过程中,当点D恰好落在
绕点A旋转过程中,当点D恰好落在 的中线
的中线 的延长线上时,延长
的延长线上时,延长 交
交 的延长线于点F,求
的延长线于点F,求 的长;
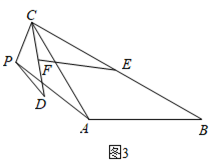
(3)
在
的长;
(3)
在 绕点A旋转过程中,探究C,D,E三点能否构成直角三角形.若能,请直接写出所有直角三角形
绕点A旋转过程中,探究C,D,E三点能否构成直角三角形.若能,请直接写出所有直角三角形 的面积;若不能,请说明理由.
的面积;若不能,请说明理由.
【考点】
三角形全等及其性质;
勾股定理;
相似三角形的判定与性质;
旋转的性质;
能力提升