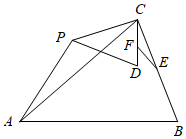
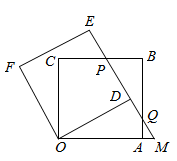
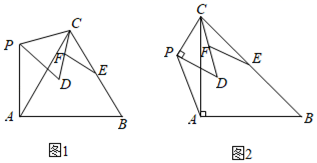
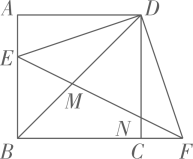
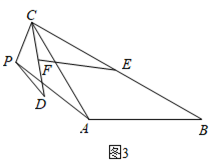
（1）观察猜想：如图1，在中，．点D是的平分线上一动点，连接，将线段绕点逆时针旋转得到线段，连接． ①的值是______；②射线与直线相交所成的较小角的度数是______．（2）类比探究如图2，在中，．点是的平分线上一动点，连接，将线段绕点逆时针旋转得到线段，连接．请写出的值及射线与直线相交所成的较小角的度数，并就图2的情形说明理由．（3）拓展延伸在（2）的条件下，若，请直接写出当时，的长为______

1. 某数学兴趣小组在测量学校旗杆的高度时，让一名同学直立在点F处，手拿一块直角三角板CDE，保持斜边CE与地面BF平行，延长CE交AB于点G，如图，并沿着射线CD的方向观察，刚好看到旗杆的顶端A点，已知该同学的身高CF为1.6米，点F到旗杆底端的距离BF为12米，CE＝0.5m，CD＝0.4m，求旗杆AB的高度．

解答题容易

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 于点D， $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ ．

计算题容易

3. 如图，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，点 $\text{[math]}$ 落在 $\text{[math]}$ 上，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

解答题容易

1.

如图1，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

（1）当 $\text{[math]}$ 绕点A旋转过程中，试探究 $\text{[math]}$ 的值；

【深入探究】

（2）如图2，点B在 $\text{[math]}$ 内部，延长 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于F，交 $\text{[math]}$ 于G，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长；

【拓展延伸】

（3）如图3，点B在 $\text{[math]}$ 内部，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于H，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 且 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

实践探究题困难

2. 数学课上，有这样一道探究题．

如图，已知 $\text{[math]}$ 中，AB=AC=m，BC=n， $\text{[math]}$ ，点P为平面内不与点A、C重合的任意一点，将线段CP绕点P顺时针旋转a，得线段PD，E、F分别是CB、CD的中点，设直线AP与直线EF相交所成的较小角为β，探究 $\text{[math]}$ 的值和 $\text{[math]}$ 的度数与m、n、α的关系，请你参与学习小组的探究过程，并完成以下任务：

(1) 问题发现：

小明研究了 $\text{[math]}$ 时，如图1，求出了 $\text{[math]}$ ， $\text{[math]}$ ；

小红研究了 $\text{[math]}$ 时，如图2，求出了 $\text{[math]}$ ， $\text{[math]}$ ；

(2) 类比探究：

他们又共同研究了α=120°时，如图3，也求出了 $\text{[math]}$ ；

归纳总结：

最后他们终于共同探究得出规律：

$\text{[math]}$ （用含m、n的式子表示）； $\text{[math]}$ （用含α的式子表示）．

(3) 求出 $\text{[math]}$ 时 $\text{[math]}$ 的值和 $\text{[math]}$ 的度数．

实践探究题困难

3. 综合与实践

背景阅读：旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动，其中“旋”是过程，“转”是结果．旋转作为图形变换的一种，具备图形旋转前后对应点到旋转中心的距离相等：对应点与旋转中心所连线段的夹角等于旋转角：旋转前、后的图形是全等图形等性质．所以充分运用这些性质是在解决有关旋转问题的关键．

实践操作：如图1，在Rt△ABC中，∠B＝90°，BC＝2AB＝12，点D，E分别是边BC，AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α．