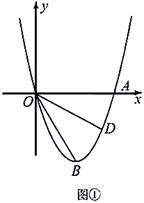
在平面直角坐标系中，抛物线经过点和点．

0 返回出卷网首页

1. 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 和点 $\text{[math]}$ ．

(1) 求该抛物线的表达式；

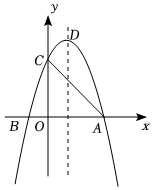
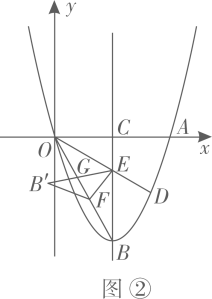
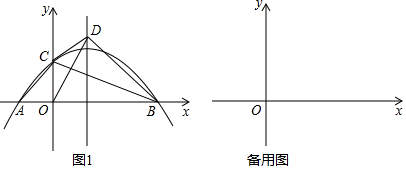
(2) 如图，该抛物线上有三个点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 轴， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与抛物线的对称轴交于点 $\text{[math]}$ （点 $\text{[math]}$ 在对称轴的左侧）．

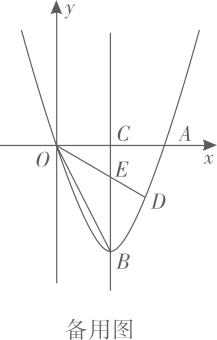
①如果点 $\text{[math]}$ 到抛物线对称轴的距离为 $\text{[math]}$ ，请用含 $\text{[math]}$ 的代数式表示点 $\text{[math]}$ 的横坐标；

②求点 $\text{[math]}$ 的横坐标．

【考点】

待定系数法求二次函数解析式; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 在平面直角坐标系 $\text{[math]}$ 中，已知：抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 和 $\text{[math]}$ ．

(1) 求抛物线的表达式；

(2) 若点 $\text{[math]}$ 在抛物线 $\text{[math]}$ 上，求 $\text{[math]}$ 的正弦值．

解答题普通

2. 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与y轴交于点C．

(1) 求该抛物线的函数解析式；

(2) 连接 $\text{[math]}$ ， $\text{[math]}$ ，点D是直线 $\text{[math]}$ 下方抛物线上的一个的动点（不与B，C重合），

①求 $\text{[math]}$ 面积的最大值；

②若 $\text{[math]}$ ，求点D的坐标．

解答题普通

3. 如图，在平面直角坐标系中， $\text{[math]}$ 的顶点E，F在x轴上， $\text{[math]}$ 且 $\text{[math]}$ ， x轴上有两点 $\text{[math]}$ ， $\text{[math]}$ ，二次函数 $\text{[math]}$ 的图象经过A、B两点，且与y轴正半轴交于点C， $\text{[math]}$ ．点 $\text{[math]}$ ．将 $\text{[math]}$ 沿x轴向左平移，平移距离为 $\text{[math]}$ ．

(1) 求a、b、c的值；

(2) 当点D首次落在抛物线上，求m的值；

(3) 当抛物线落在 $\text{[math]}$ 内的部分，满足y随x的增大而增大时，请直接写出m的取值范围．

解答题普通