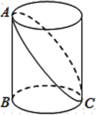
如图，一只蚂蚁从长为、宽为、高为的长方体纸箱的点沿纸箱表面爬到点，那么它所爬行的最短路线的长是（）

0 返回出卷网首页

1. 如图，一只蚂蚁从长为 $\text{[math]}$ 、宽为 $\text{[math]}$ 、高为 $\text{[math]}$ 的长方体纸箱的 $\text{[math]}$ 点沿纸箱表面爬到 $\text{[math]}$ 点，那么它所爬行的最短路线的长是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

两点之间线段最短; 勾股定理的实际应用-最短路径问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，用7个棱长为1的正方体搭成一个几何体，沿着该几何体的表面从点M到点N的所有路径中，最短路径的长是（）

A. 5 B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 数学教育家波利亚曾说：“对一个数学问题，改变它的形式，变换它的结构，直到发现有价值的东西，这是数学解题的一个重要原则”．在复习二次根式时，老师提出了一个求代数式最小值的问题，如： “当 $\text{[math]}$ 时，求代数式 $\text{[math]}$ 的最小值”，其中 $\text{[math]}$ 可看作两直角边分别为x和2的 $\text{[math]}$ 的斜边长， $\text{[math]}$ 可看作两直角边分别是 $\text{[math]}$ 和3的 $\text{[math]}$ 的斜边长．于是构造出如图，将问题转化为求 $\text{[math]}$ 的最小值，运用此方法，请你解决问题：已知x，y均为正数，且 $\text{[math]}$ ．则 $\text{[math]}$ 的最小值是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. 6

单选题容易

3. 如图，直线l是一条河，P，Q两地相距8km，P，Q两地到l的距离分别为2km，5km，欲在l上的某点M处修建一个水泵站，向P，Q两地供水．现有如下四种铺设方案，图中实线表示铺设的管道，则铺设的管道最短的是（　　）.

单选题容易