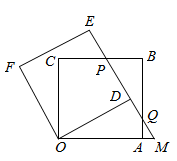
1.
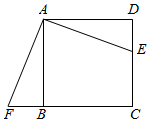
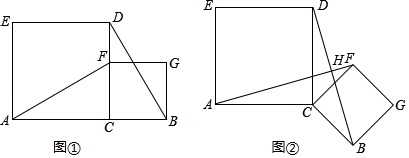
如图,E是正方形 边
边 的上一点,将
的上一点,将 绕点A旋转
绕点A旋转 得到
得到 , 过点A作
, 过点A作 的垂线分别交
的垂线分别交 、
、 于H、G.若
于H、G.若 ,
,  , 则
, 则 .(用含n的式子表示)
.(用含n的式子表示)

【考点】
勾股定理;
正方形的性质;
旋转的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练