1.
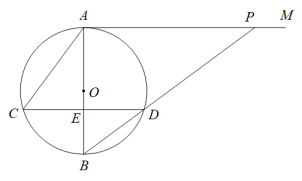
据史料记载,马车的发明者是 多年前生活于夏王朝初年的奚仲.马车的发明是中国科技史上的一大创举.如图是古代马车的侧面示意图,
多年前生活于夏王朝初年的奚仲.马车的发明是中国科技史上的一大创举.如图是古代马车的侧面示意图, 是车轮
是车轮 的直径,过圆心O的车架
的直径,过圆心O的车架 的一端点C着地时,水平地面
的一端点C着地时,水平地面 与车轮
与车轮 相切于点D,连接
相切于点D,连接 .
.

(1)
若 , 求
, 求 的度数;
(2)
若
的度数;
(2)
若 ,
,  , 求车轮的半径长.
, 求车轮的半径长.
【考点】
勾股定理;
圆周角定理;
切线的性质;