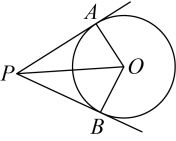
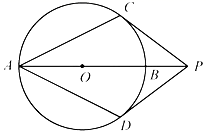
如图，PA，PB分别与相切于点A，B，连结OP．则下列判断错误的是（）

0 返回出卷网首页

1. 如图，PA，PB分别与 $\text{[math]}$ 相切于点A，B，连结OP．则下列判断错误的是（）

A. ∠PA0=∠PB0=90 $\text{[math]}$ B. OP平分∠APB C. PA=PB D. $\text{[math]}$

【考点】

切线的性质; 切线长定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图， $\text{[math]}$ 与 $\text{[math]}$ 分别切 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的直径，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，下列说法错误的是（）

A. $\text{[math]}$ B. 若 $\text{[math]}$ ，则 $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 如图， $\text{[math]}$ 分别与 $\text{[math]}$ 相切于A、B两点，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，AB是⊙O的切线，B为切点，AO与⊙O交于点C，若∠BAO=40°，则∠OCB的度数为（）

A. 40° B. 50° C. 65° D. 75°

单选题容易