在解决数学问题时，我们常常从特殊入手，猜想结论，并尝试发现解决问题的策略与方法．【问题提出】求证：如果一个定圆的内接四边形对角线互相垂直，那么这个四边形的对边的平方和是一个定值．

0 返回出卷网首页

1. 在解决数学问题时，我们常常从特殊入手，猜想结论，并尝试发现解决问题的策略与方法．

【问题提出】

求证：如果一个定圆的内接四边形对角线互相垂直，那么这个四边形的对边的平方和是一个定值．

(1) 【从特殊入手】

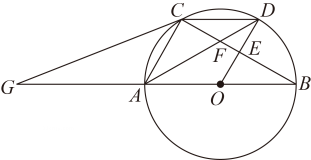
我们不妨设定圆O的半径是R，⊙O的内接四边形ABCD中，AC⊥BD．

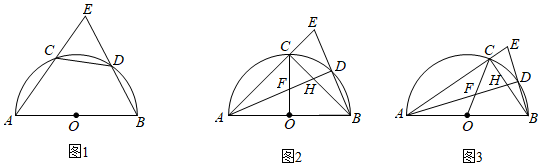
请你在图①中补全特殊殊位置时的图形，并借助于所画图形探究问题的结论．

(2) 【问题解决】

已知：如图②，定圆⊙O的半径是R，四边形ABCD是⊙O的内接四边形，AC⊥BD．

求证：AB²＋CD²＝BC²＋AD²＝4R²

【考点】

勾股定理; 圆周角定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ ．

(1) 求 $\text{[math]}$ 的度数；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长度．

解答题普通

2. 如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为这边上的“奇特三角形”，这条边称为“奇特边”.

（1）如图1，已知△ABC是奇特三角形， $\text{[math]}$ ，且∠C＝90°.

①△ABC的奇特边是；

②设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求a：b：c；

（2）如图2，AM是△ABC的中线，若△ABC是BC边上的奇特三角形，找出BC²与AB²＋AC²之间的关系；

（3）如图3，在四边形ABCD中，∠B=90°（AB<BC）， $\text{[math]}$ ，对角线AC把它分成了两个奇特三角形，且△ACD是以AC为腰的等腰三角形，求等腰△ACD的底边长.

解答题困难

3. 如图，已知一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象在第一、第三象限分别交于 $\text{[math]}$ ， $\text{[math]}$ 两点，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于 $\text{[math]}$ 两点．

（1）求一次函数和反比例函数的解析式；

（2）比较大小： $\text{[math]}$ 　　 $\text{[math]}$ （填“＞”或“＜”或“＝”）；

（3）直接写出 $\text{[math]}$ 时 $\text{[math]}$ 的取值范围．

解答题普通