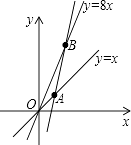
如图，一次函数的图象与x轴交于点A(1，0)，它与x轴所成的锐角为α，且tanα＝，则此一次函数表达式为.

0 返回出卷网首页

1. 如图，一次函数的图象与x轴交于点A(1，0)，它与x轴所成的锐角为α，且tanα＝ $\text{[math]}$ ，则此一次函数表达式为.

【考点】

待定系数法求一次函数解析式; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 在平面直角坐标系中，一次函数y＝kx+b（k、b为常数，且k≠0）的图象如图所示，根据图象中的信息可求得关于x的方程kx+b＝﹣1的解为．

填空题容易

2. 已知直线l：y=（3-k）x+1经过点（4，9），则它的解析式为.

填空题容易

3. 请写出一个图象经过点 $\text{[math]}$ ，且y随x的增大而减小的函数解析式：．

填空题容易