1.
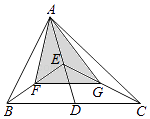
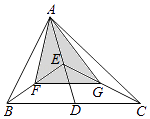
如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是( )
A.
4.5
B.
5
C.
5.5
D.
6
【考点】
三角形的面积;
三角形的中位线定理;