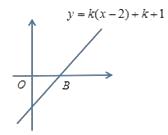
如图，直线y= x+2交x轴于点A，交y轴于点B，点P（x，y）是线段AB上一动点（与A，B不重合），△PAO的面积为S，求S与x的函数关系式，并写出自变量的取值范围.

0 返回出卷网首页

1. 如图，直线y= $\text{[math]}$ x+2交x轴于点A，交y轴于点B，点P（x，y）是线段AB上一动点（与A，B不重合），△PAO的面积为S，求S与x的函数关系式，并写出自变量的取值范围.

【考点】

一次函数图象与坐标轴交点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 已知一次函数y＝kx＋b的图象经过点A(―1，3)和点B(2，―3)．

(1)求这个一次函数的表达式；

(2)求直线AB与坐标轴围成的三角形的面积．

解答题容易

2. 已知直线 $\text{[math]}$ 经过点 $\text{[math]}$ ，求此直线与x轴，y轴的交点坐标．

解答题容易

3. 如图，一次函数y $\text{[math]}$ x+6与坐标轴交于A、B两点，求点A、B的坐标.

解答题容易